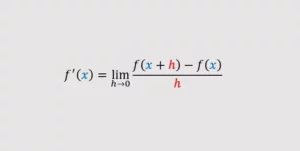Ejercicio 1: Halla la derivada de la siguiente función f(x)=x2+1 en x = 1, aplicando la definición de derivada.
Solución:
Utilizando la fórmula
f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}Si f(x) es x2+1entonces f(x+h)=(x+h)2+1 y sustituimos en la fórmula:
f'(x)=\lim_{h \to 0}\frac{(x+h)^2+1-(x^2+1)}{h}Resolvemos el binomio al cuadrado:
f'(x)=\lim_{h \to 0}\frac{x^2+2xh+h^2+1-x^2-1}{h}Reducimos los términos
f'(x)=\lim_{h \to 0}\frac{\cancel{x^2}+2xh+h^2+\cancel{1}-\cancel{x^2}-\cancel{1}}{h}f'(x)=\lim_{h \to 0}\frac{2xh-h^2}{h}Separamos la fracción y volvemos a reducir:
f'(x)=\lim_{h \to 0}\frac{2x\cancel{h}}{\cancel{h}}-\frac{h^{\cancel{2}}}{\cancel{h}}f'(x)=\lim_{h \to 0}2x-hAhora sustituimos el valor de h = 0
f'(x)=2x-(0)
La derivada es :
f'(x)=2x
Ahora valuamos en x=1
f'(1)=2(1)
La derivada en x=1 es 2
f'(1)=2
Ejercicio 2: Calcula la derivada de la siguiente función f(x)=1/x, aplicando la definición de derivada.
Solución:
Utilizando la fórmula
f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}Si f(x) es 1/x entonces f(x+h)=1/x+h y sustituimos en la fórmula:
f'(x)=\lim_{h \to 0}\frac{\frac{1}{x+h}-\frac{1}{x}}{h}Resolvemos la fracción:
f'(x)=\lim_{h \to 0}\frac{\frac{x-(x+h)}{x(x+h)}}{h}Reducimos los términos
f'(x)=\lim_{h \to 0}\frac{\frac{x-x-h}{x(x+h)}}{h}Aplicamos la división
f'(x)=\lim_{h \to 0}\frac{\frac{x-x-h}{x(x+h)}}{\frac{h}{1}}f'(x)=\lim_{h \to 0}\frac{x-x-h}{h\cdot x(x+h)}Reducimos términos:
f'(x)=\lim_{h \to 0}\frac{\cancel{x}-\cancel{x}-\cancel{h}}{\cancel{h}\cdot x(x+h)}f'(x)=\lim_{h \to 0}\frac{-1}{ x(x+h)}Ahora sustituimos el valor de h = 0
f'(x)=\frac{-1}{ x(x+0)}La derivada es :
f'(x)=-\frac{1}{ x^2}Ejercicio 3: obtener la derivada por definición de la siguiente función f(x)=x/x+1.
Solución:
Utilizando la fórmula
f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}Si f(x) es x/x+1 entonces f(x+h)=(x+h)/(x+h)+1 y sustituimos en la fórmula:
f'(x)=\lim_{h \to 0}\frac{\frac{x+h}{x+h+1}-\frac{x}{x+1}}{h}Resolvemos la fracción:
f'(x)=\lim_{h \to 0}\frac{\frac{(x+1)(x+h)-(x)(x+h+1)}{x+1(x+h+1)}}{h}Resolvemos la multiplicación de los binomios
f'(x)=\lim_{h \to 0}\frac{\frac{x^2+xh+x+h-x^2-xh-x}{x+1(x+h+1)}}{h}Reducimos términos
f'(x)=\lim_{h \to 0}\frac{\frac{\cancel{x^2}+\cancel{xh}+\cancel{x}+h-\cancel{x^2}-\cancel{xh}-\cancel{x}}{x+1(x+h+1)}}{h}f'(x)=\lim_{h \to 0}\frac{\frac{h}{x+1(x+h+1)}}{h}Aplicamos la división
f'(x)=\lim_{h \to 0}\frac{\frac{h}{x+1(x+h+1)}}{\frac{h}{1}}f'(x)=\lim_{h \to 0}\frac{1}{x+1(x+h+1)}Ahora sustituimos el valor de h = 0
f'(x)=\frac{1}{x+1(x+0+1)}f'(x)=\frac{1}{(x+1)(x+1)}Del denominador (x+1)(x+1) es igual a (x+1)2 por tanto la derivada es:
f'(x)=\frac{1}{ (x+1)^2}