A continuación te presento ejercicios resueltos de suma de vectores paso a paso.
Ejercicio 1: Suma de vectores
Tres sogas están atadas a una estaca, sobre la cual actúan tres fuerzas: A=25 N, este; B=35 N, 30⁰ NO; y C=45 N, 56⁰ SO. Determinar la fuerza resultante.
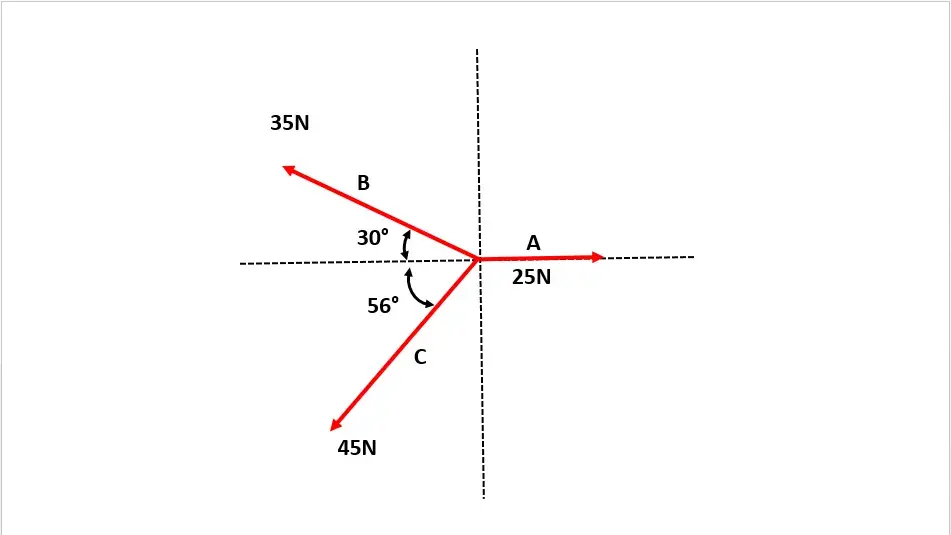
Como primer paso realizaremos la descomposición vectorial en su componentes X y Y
\text{Compenentes} \ x \\
Ax=25cos0\\Ax=25NBx=-35cos30\\Bx=-30.31N
Cx=-45cos56\\Cx=-25.16N
\text{Compenentes} \ y \\
Ay=25sen0\\Ay=0 NBy=35sen30\\By=17.5N
Cy=-45sen56\\Cy=-37.30N
Segundo paso:
\text{Sumatoria de las componentes en} \ x \left(\sum{x}\right)\ \text{y las componentes en } \ y \left(\sum{y}\right)\sum{x}\sum{x}=ax+bx+cy\sum{x}=25N-30.31N-25.26N \sum{x}=-30.47N \sum{y}\sum{y}=ay+by+cy\sum{y}=0N+17.5N-37.3N \sum{y}=-19.8N Tercer paso:
Obtención del vector resultante R
R=\sqrt{\left(\sum{x}\right)^2+\left(\sum{y}\right)^2}R=\sqrt{\left(-30.47\right)^2+\left(-19.8\right)^2}R=36.38N
Cuarto paso:
Obtención de la dirección (ángulo) del vector resultante:
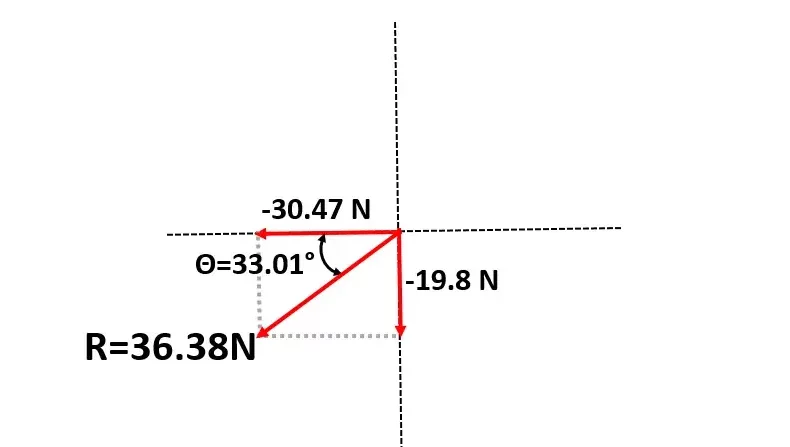
\theta=tan^{-1}\left(\frac{\sum{y}}{\sum{x}}\right)\theta=tan^{-1}\left(\frac{19.8}{-30.47}\right)\theta=33.01°
Ejercicio 2: Suma de vectores
Dos fuerzas actúan sobre el automóvil ilustrado en la figura. La fuerza a es igual a 130 N, hacia el oeste, y la fuerza B es igual a 215 N a 60⁰ NO. ¿Cuáles son la magnitud y la dirección de la fuerza resultante sobre el automóvil?
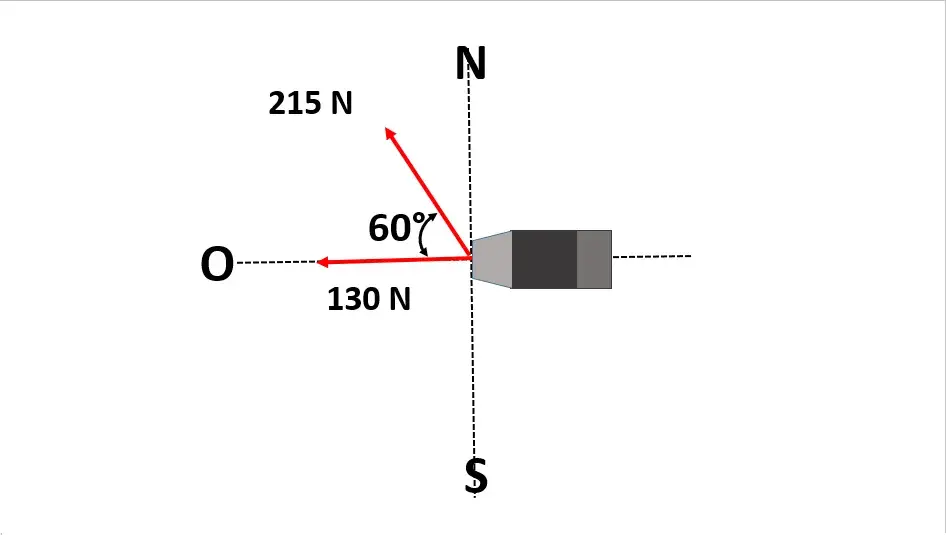
Como primer paso realizaremos la descomposición vectorial en su componentes X y Y
\text{Compenentes} \ x \\
Ax=-130cos0\\Ax-130NBx=-215cos60\\Bx=-107.5N
\text{Compenentes} \ y \\
Ay=130sen0\\Ay=0 NBy=215sen60\\By=186.19N
Segundo paso:
\text{Sumatoria de las componentes en} \ x \left(\sum{x}\right)\ \text{y las componentes en } \ y \left(\sum{y}\right)\sum{x}\sum{x}=ax+bx\sum{x}=-130N-107.5N\sum{x}=-237.55N\sum{y}\sum{y}=ay+by\sum{y}=0N+186.19N \sum{y}=186.19N Tercer paso:
Obtención del vector resultante R
R=\sqrt{\left(\sum{x}\right)^2+\left(\sum{y}\right)^2}R=\sqrt{\left(-237.5\right)^2+\left(186.19\right)^2}R=301.7N
Cuarto paso:
Obtención de la dirección (ángulo) del vector resultante:
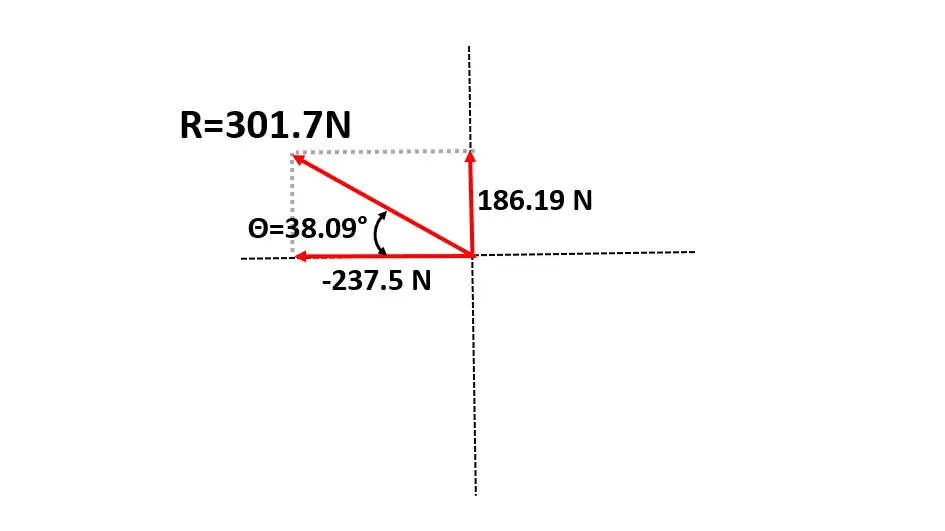
\theta=tan^{-1}\left(\frac{\sum{y}}{\sum{x}}\right)\theta=tan^{-1}\left(\frac{186.19}{-237.5}\right)\theta=-38.09°
Nota: el ángulo es negativo porque abre en dirección de las manecillas del reloj.
Ejercicio 3: Suma de vectores
Calcula la fuerza resultante y su ángulo, la cual actúa sobre el perno de la siguiente figura.
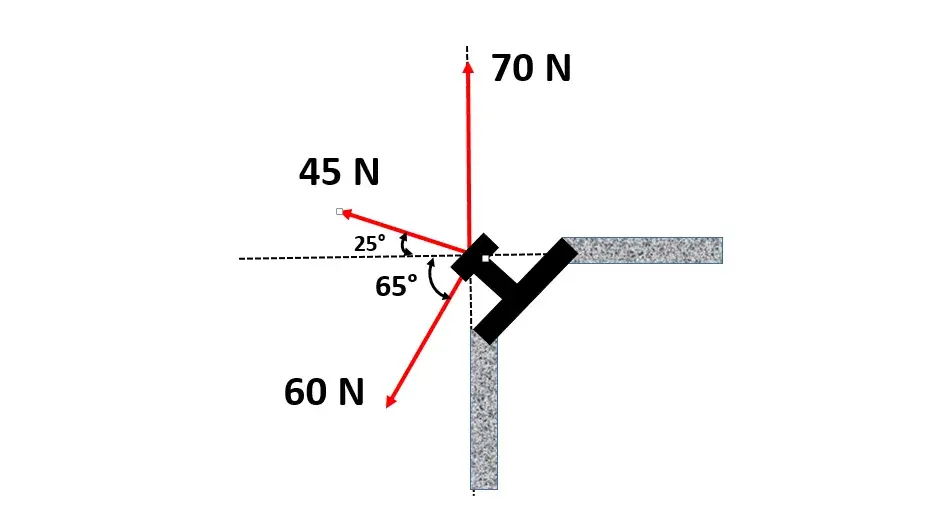
Como primer paso realizaremos la descomposición vectorial en su componentes X y Y
\text{Compenentes} \ x \\
Ax=70cos90\\Ax=0NBx=-45cos25\\Bx=-40.78N
Cx=-60cos65\\Cx=-25.35N
\text{Compenentes} \ y \\
Ay=70sen90\\Ay=70 NBy=45sen25\\By=19.01N
Cy=-60sen65\\Cy=-54.37N
Segundo paso:
\text{Sumatoria de las componentes en} \ x \left(\sum{x}\right)\ \text{y las componentes en } \ y \left(\sum{y}\right)\sum{x}\sum{x}=ax+bx+cy\sum{x}=0N-40.78N-25.35N\sum{x}=-66.13N \sum{y}\sum{y}=ay+by+cy\sum{y}=70N+19.01N-54.37N\sum{y}=34.64N Tercer paso:
Obtención del vector resultante R
R=\sqrt{\left(\sum{x}\right)^2+\left(\sum{y}\right)^2}R=\sqrt{\left(-66.13\right)^2+\left(34.6\right)^2}R=74.65N
Cuarto paso:
Obtención de la dirección (ángulo) del vector resultante:
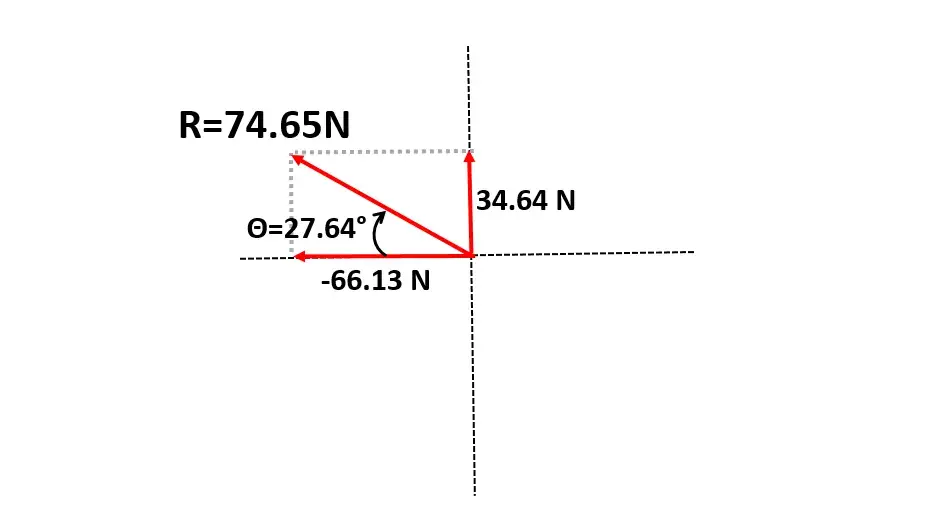
\theta=tan^{-1}\left(\frac{\sum{y}}{\sum{x}}\right)\theta=tan^{-1}\left(\frac{34.64}{-66.13}\right)\theta=-27.64°
Si necesitas una asesoría presencial o en línea contáctanos y síguenos por Facebook, Tiktok e Instagram