Suma de vectores método analítico

Para explicar las Suma de vectores método analítico, primero explicaremos que es un vector.

¿Qué es un vector?

  • Un vector es todo segmento de recta dirigido en el espacio.  Las magnitudes vectoriales se representan gráficamente mediante flechas.
  •  Es una línea en un plano que representa una magnitud física, indicada por la longitud del vector, la dirección que  está dada por el ángulo del vector y por último el sentido que nos lo indica la flecha.

Este se caracteriza por tener:

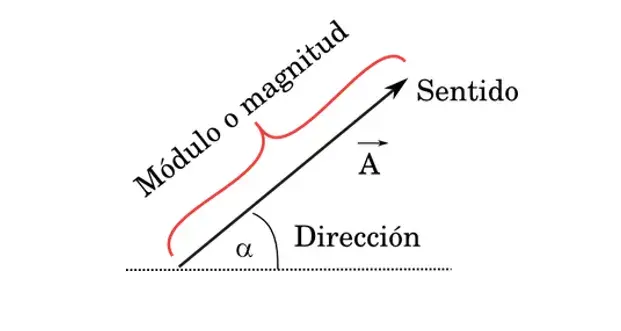
Vector

Magnitud o Módulo

Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, debemos medir desde su origen hasta su extremo.

Dirección

Es la orientación en el espacio de la recta que lo contiene, es el ángulo.

Sentido

Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.

Suma de vectores método analítico

La suma gráfica de vectores a veces no tiene la exactitud suficiente ya que con regla y transportador no no es útil y más cuando los vectores están en tres dimensiones.

Todo vector puede descomponerse como la suma de otros dos vectores, llamados componentes vectoriales del vector original.

Para poder hacer la suma de vectores, primero tenemos que realizar la descomposición vectorial de cada vector.

Descomposición vectorial

Para realizar la descomposición vectorial utilizaremos herramientas trigonométricas

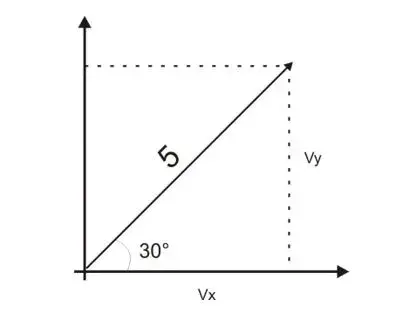
Para obtener Vx

 \\cos\theta=\frac{C.A}{h}
 cos30°=\frac{Vx}{5}
\text{Despejando} \ Vx  \\
Vx=5cos30\\Vx=4.33

Para obtener Vy

\\sen\theta=\frac{C.O}{h}
sen30°=\frac{Vy}{5}
\text{Despejando} \ Vx \\
Vy=5sen30\\Vx=2.5

A partir del siguiente ejercicio se explicará paso a paso la suma en forma analítica.

Primer paso:

Descomposición Vectorial en sus componentes x, y

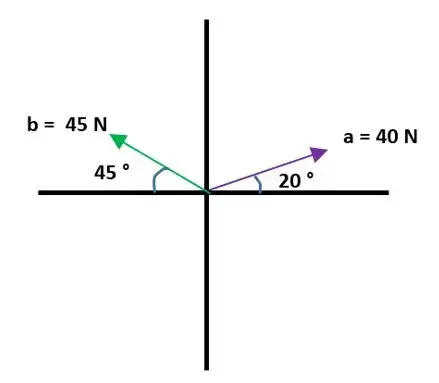
Suma de vectores

Componente x

\\ax=40cos20 \\ ax=37.58 N
bx=-45cos45 \\bx=-31.81N

Componente x

\\ay=40sen20 \\ay=13.68 N
by=45cos45 \\by=31.81N

Segundo paso:

Sumatoria de las componentes en X y Y 

\sum{x}
\sum{x}=ax+bx
\sum{x}=37.58N-31.81N  
\sum{x}=5.77N  
\sum{y}
\sum{y}=ay+by
\sum{y}=13.68N+31.81N    
\sum{y}=45.49N

Tercer paso:

Obtención del vector resultante R

R=\sqrt{\left(\sum{x}\right)^2+\left(\sum{y}\right)^2}
R=\sqrt{\left(5.77\right)^2+\left(45.49\right)^2}
R=45.85N

Cuarto paso:

Obtención de la dirección (ángulo) del vector resultante:

\theta=tan^{-1}\left(\frac{\sum{y}}{\sum{x}}\right)
\theta=tan^{-1}\left(\frac{45.49}{5.77}\right)
\theta=82.77°

Sígueme por Facebook, Tiktok, Twitter e Instagram