En este artículo resolveré problemas paso a paso de diferentes ejercicios relacionados con ecuación de la circunferencia.
Ejercicio 1: Hallar la ecuación de la circunferencia que tiene el centro en el punto C(-4,-1) y es tangente a la recta 3x+2y+2=0
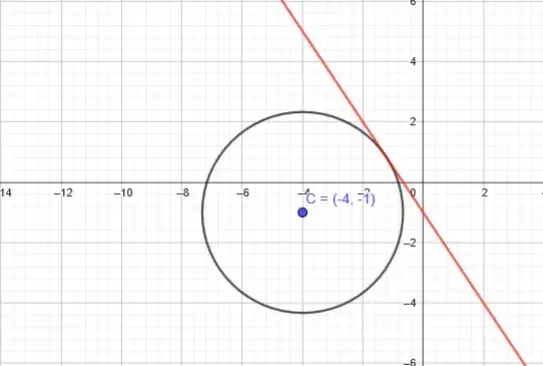
Para poder encontrar la ecuación debemos conocer el radio, para esto utilizaremos la fórmula de distancia de un punto a una recta
D=\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}La ecuación general de la recta es Ax + By + C = 0, Los elementos conocidos entonces son:
De la ecuación 3x+2y+2=0; A=3, B=3, C=2. Del punto C ( -4 , -1 ); x1=-4, y1=-1.
D=\frac{|(3)(-4)+(2)(-1)+2|}{\sqrt{(3)^2+(2)^2}}D=\frac{|-12-2+2|}{\sqrt{9+4}}D=\frac{|-12|}{\sqrt{13}}La distancia que hay del centro a la recta es el radio de la circunferencia, por lo tanto r es:
r=\frac{12}{\sqrt{13}}Ahora se sustituye en la fórmula de la ecuación de la circunferencia en su forma ordinaria
(x-h)^2+(y-k)^2=r^2
Donde h y k son las coordenadas del centro de la circunferencia.
(x-(-4))^2+(y-(-1))^2=\left(\frac{12}{\sqrt{13}}\right)^2(x+4)^2+(y+1)^2=\left(\frac{12}{\sqrt{13}}\right)^2Resolvemos los cuadrados
x^2+8x+16+y^2+2y+1=\frac{144}{13}x^2+8x+16+y^2+2y+1-\frac{144}{13}=0La ecuación de la circunferencia es:
x^2+y^2+8x+2y+\frac{77}{13}=0Ejercicio 2: Determinar el centro, radio y la ecuación de la circunferencia y lugar geométrico de una circunferencia que tiene como diámetro la cuerda limitada por los puntos: A(2,-2) y B(8,-2)
Primero calculamos el punto medio que hay entre el punto A y B, el cual es el centro de la circunferencia.
Fórmula de punto medio.
P_m= \left( \frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)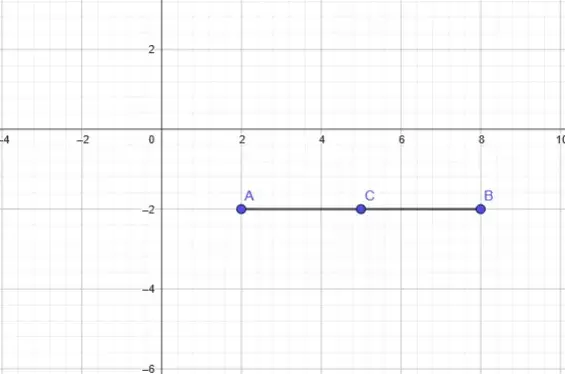
Sustituimos los puntos A (2,-2) y B (8,-2)
P_m= \left( \frac{2+8}{2}, \frac{-2-2}{2}\right)P_m= \left( 5, -2\right)
El centro de la circunferencia es c ( 5 , -2 )
Para encontrar el radio, utilizaremos la fórmula de distancia del centro al punto A o B
d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}La distancia entre el punto c ( 5 , -2 ) y A (2,-2).
d=\sqrt{(2-5)^2+(-2-(-2))^2}d=\sqrt{(-3)^2+(0)^2}d=\sqrt{9}Por lo tanto el radio r es:
r=3
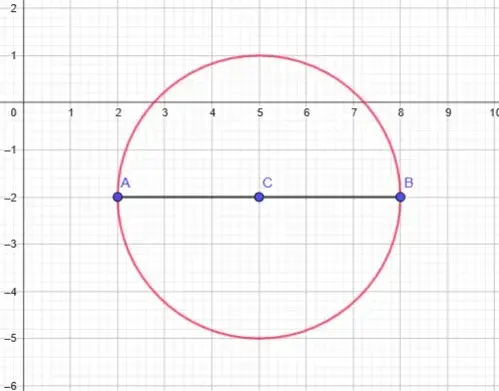
Ahora se sustituye el centro c ( 5 , -2 ) y el radio r=3 en la fórmula de la ecuación en su forma ordinaria
(x-h)^2+(y-k)^2=r^2
(x-5)^2+(y-(-2))^2=3^2
(x-5)^2+(y+2)^2=3^2
Resolvemos los cuadrados
x^2-10x+25+y^2+4y+4=9
x^2+y^2-10x+4y+25+4-9=0
La ecuación de la circunferencia es:
x^2+y^2-10x+4y+20=0
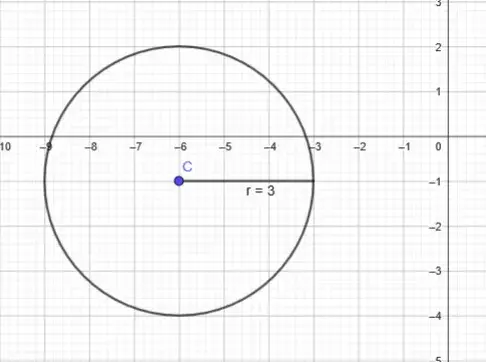
Ejercicio 3. Hallar el centro y el radio de la circunferencia x2+y2+12x+2y+28=0
Para resolver el ejercicio debemos debemos completar cuadrados
x^2+12x+36+y^2+2y+1=-28+36+1
x^2+12x+36+y^2+2y+1=9
Factorizamos los trinomios cuadrados perfectos.
(x+6)^2+(y+1)^2=3^2
El centro c = ( -6 , -1 ) y el radio r = 3