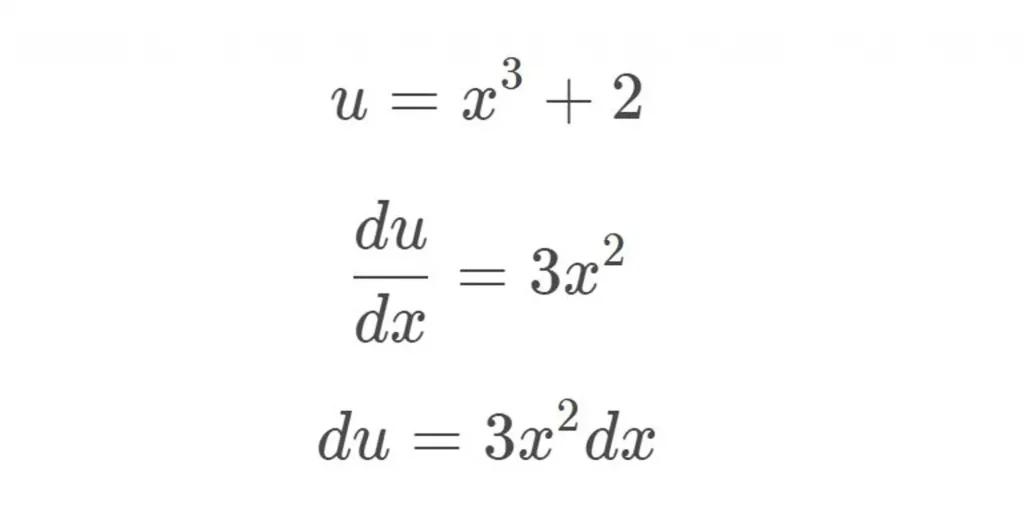
Integrales paso a paso apoyándonos con un cambio de variable
En este post resolveremos integrales paso a paso apoyándonos con un cambio de variable
Ejercicio 1
\int \left(x^3+2\right)^23x^2dx
Para el cambio de variable tomaremos el binomio como u:
x^3+2=u
Ahora obtenemos du, derivando u y despejando el diferencial
u=x^3+2
\frac{du}{dx}=3x^2du=3x^2dx
Aplicamos la fórmula de la integral
\int u^n du= \frac{u^{n+1}}{n+1}+c \int u^2 du= \frac{u^{2+1}}{2+1}+c = \frac{u^{3}}{3}+c Regresamos la variable
\frac{u^{3}}{3}+c=\frac{\left(x^3+2\right)^3}{3}+cEjercicio 2
\int \left(x^3+2\right)^\frac{1}{2}x^2dxPara el cambio de variable tomaremos el binomio como u:
x^3+2=u
Ahora obtenemos du, derivando u y despejando el diferencial
u=x^3+2
\frac{du}{dx}=3x^2du=3x^2dx
Como podemos ver el diferencial es
du=3x^2dx
Y el de nuestra integral le falta el 3
\int \left(x^3+2\right)^\frac{1}{2}\textcolor{blue}{x^2dx}Para completar la diferencial ponemos el tres pero también dividimos entre tres
\int \left(x^3+2\right)^\frac{1}{2}\textcolor{blue}{\frac{3}{3}x^2dx}=\textcolor{blue}{\frac{1}{3}}\int \left(x^3+2\right)^\frac{1}{2}\textcolor{blue}{3x^2dx} Ahora aplicamos la fórmula de la integral
\int u^n du= \frac{u^{n+1}}{n+1}+c \frac{1}{3} \int u^{\frac{1}{2}}du= \frac{1}{3}\left[ \frac{u^{\frac{1}{2}+1}}{\frac{1}{2}+1} \right]+c =\frac{1}{3} \left[ \frac{u^{\frac{3}{2}}}{\frac{3}{2}} \right] +c=\frac{1}{3}\left[ \frac{2u^{\frac{3}{2}}}{3}\right]+c=\frac{2u^{\frac{3}{2}}}{9}+cRegresamos la variable
\frac{2u^{\frac{3}{2}}}{9}+c=\frac{2\left( x^3+2 \right)^\frac{3}{2}}{9}+cEjercicio 3
\int \frac{8x^2dx}{\left(x^3-2\right)^3}Subimos el binomio al cuadrado al numerador
8\int \left(x^3-2 \right)^{-3}dxPara el cambio de variable tomaremos el binomio como u:
x^3-2=u
Ahora obtenemos du, derivando u y despejando el diferencial
u=x^3-2
\frac{du}{dx}=3x^2du=3x^2dx
Como podemos ver el diferencial es
du=3x^2dx
Y a nuestra integral le falta el 3
8\int \left(x^3-2\right)^{-3}\textcolor{blue}{x^2dx}Para completar la diferencial ponemos el tres pero también dividimos entre tres
8\int \left(x^3-2\right)^{-3}\textcolor{blue}{\frac{3}{3}x^2dx}==8*\textcolor{blue}{\frac{1}{3}}\int \left(x^3-2\right)^{-3}\textcolor{blue}{3x^2dx} Ahora aplicamos la fórmula de la integral
\int u^n du= \frac{u^{n+1}}{n+1}+c \frac{8}{3}\int u^{-3}du= \frac{8}{3}\left[ \frac{u^{-3+1}}{-3+1} \right]+c =\frac{8}{3}\left[ \frac{u^{-2}}{-2}\right]+c=-\frac{8u^{-2}}{6}+c=-\frac{4u^{-2}}{3}+cRegresamos la variable
-\frac{4u^{-2}}{3}+c=-\frac{4\left( x^3-2 \right)^{-2}}{3}+cEjercicio 4
\int3x\sqrt{1-2x^{2}}dxPara empezar el radical lo expresamos como potencia:
3\int \left(1-2x^2\right)^\frac{1}{2}xdxPara el cambio de variable tomaremos el binomio como u:
1-2x^2=u
Ahora obtenemos du, derivando u y despejando el diferencial
u=1-2x^2
\frac{du}{dx}=-4xdu=-4xdx
Como podemos ver el diferencial es
du=-4xdx
Y a nuestra integral le falta el -4
3\int \left(1-x^2\right)^\frac{1}{2}\textcolor{blue}{xdx}Para completar la diferencial ponemos el -4 pero también dividimos entre -4
3\int \left(1-x^2\right)^\frac{1}{2}\textcolor{blue}{\frac{-4}{-4}xdx}==\textcolor{blue}{-\frac{1}{4}}*3\int \left(1-x^2\right)^\frac{1}{2}*\textcolor{blue}{-4xdx} =\textcolor{blue}{-\frac{3}{4}}\int \left(1-x^2\right)^\frac{1}{2}*\textcolor{blue}{-4xdx} Ahora aplicamos la fórmula de la integral
\int u^n du= \frac{u^{n+1}}{n+1}+c -\frac{3}{4}\int u^\frac{1}{2}= -\frac{3}{4}\left[ \frac{u^{\frac{1}{2}+1}}{\frac{1}{2}+1} \right]+c =-\frac{3}{4} \left[ \frac{u^{\frac{3}{2}}}{\frac{3}{2}} \right] +c=-\frac{3}{4}\left[ \frac{2u^{\frac{3}{2}}}{3}\right]+c-\frac{6u^{\frac{3}{2}}}{12}+c=-\frac{u^{\frac{3}{2}}}{2}+cRegresamos la variable
-\frac{u^{\frac{3}{2}}}{2}+c=-\frac{\left( 1-x^2 \right)^\frac{3}{2}}{2}+cEjercicio 5
\int \frac{\left(x+3\right)dx}{\left(x^2+6x\right)^{\frac{1}{3}}}dxSubimos el binomio al cuadrado al numerador
\int \left(x^2+6x\right)^{-\frac{1}{3}}\left(x+3 \right)dxPara el cambio de variable tomaremos el binomio como u:
x^2+6x=u
Ahora obtenemos du, derivando u y despejando el diferencial
u=x^2+6x
\frac{du}{dx}=2x+6du=\left(2x+6\right)dx
Podemos factorizar 1/2
du=\frac{1}{2}\left(x+3\right)dxComo podemos ver ya tenemos completo nuestra integral
\frac{1}2{}\int \left(x^2+6x\right)^{-\frac{1}{3}}\textcolor{blue}{\left(x+3 \right)dx}Ahora aplicamos la fórmula de la integral
\int u^n du= \frac{u^{n+1}}{n+1}+c \frac{1}{2} \int u^{-\frac{1}{3}}du= \frac{1}{2}\left[ \frac{u^{-\frac{1}{3}+1}}{-\frac{1}{3}+1} \right]+c =\frac{1}{2} \left[ \frac{u^{\frac{2}{3}}}{\frac{2}{3}} \right] +c=\frac{1}{2}\left[ \frac{3u^{\frac{2}{3}}}{2}\right]+c=\frac{3u^{\frac{2}{3}}}{4}+cRegresamos la variable
\frac{3u^{\frac{2}{3}}}{4}+c=\frac{3\left( x^2+6x \right)^\frac{2}{3}}{4}+c