Sucesiones cuadráticas

Las sucesiones cuadráticas son una serie de números en la cual las diferencias entre términos consecutivos que no son constantes (del primer nivel), pero las segundas diferencias sí lo son (del segundo nivel). Esto se debe a que los términos de la sucesión siguen una fórmula.

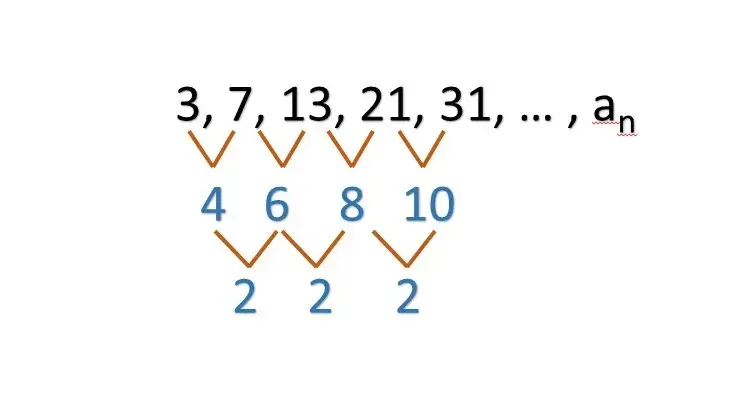
Cada uno de los números de nuestra sucesión se le denomina término el cual se representa como t_n, y cada n representa cada unos de las posiciones en la que se encuentra nuestro término, así que el término t₁ es 3; el término t₂ es 7; el término t₃ es 13; el término t₄ es 21; el término t₅ es 7.

Para calcular cualquier término t_n se calcula mediante la siguiente fórmula:

t_{n}=an^{2}+bn+c

Para obtener a, b y c, es necesario desarrollar las diferencias de los dos niveles de nuestra sucesión

Ahora lo ejemplificaré paso a paso cualquier término de las sucesiones cuadráticas con el siguiente ejercicio.

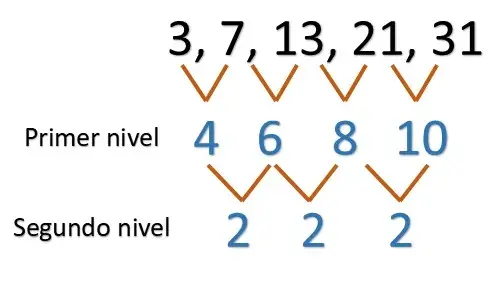
Encontrar la regla general de la siguiente sucesión: 3, 7, 13, 21, 31…

Como primer paso es calcular las diferencias que hay entre cada numero de nuestra sucesión, así encontramos el primer nivel.

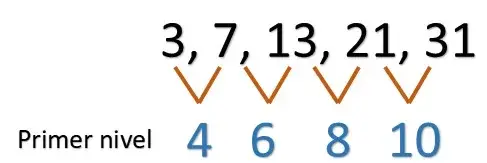
El segundo paso es calcular las diferencias que hay entre cada número del primer nivel:

La forma general para encontrar cualquier termino es :

t_{n}=an^{2}+bn+c

Para obtener a, b y c vamos a utilizar las siguientes ecuaciones:

2a=\text{ al primer número del segundo nivel}

3a+b=\text{ al primer número del primer nivel}

a+b+c=\text{ al primer número de la sucesión}

Esto es:

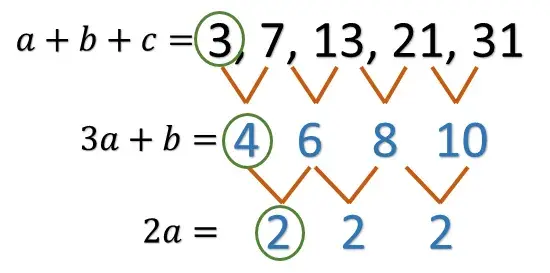
Las ecuaciones nos quedan:

2a=2

3a+b=4

a+b+c=3

Resolvemos las ecuaciones :

2a=2

a=\frac{2}{2}=1

Sustituimos a=1 en la ecuación

3a+b=4

3(1)+b=4

3+b=4

b=4-3=1

Ahora resolvemos la ultima ecuación, sustituyendo a=1 y b=1

a+b+c=3

(1)+(1)+c=3

2+c=3

c=3-2=1

Ya que tenemos los valores de a, b y c los sustituimos en la fórmula general.

t_{n}=an^{2}+bn+c

Para a=1, b=1 y c=1

t_{n}=(1)n^{2}+(1)n+1

Nuestro termino t_n nos queda:

t_{n}=n^{2}+n+1

Ahora vamos a comprobar que nuestro resultado cumple para cualquiera de los términos, para esto calcularemos el termino que esta en la posición 3 de nuestra sucesión (3, 7, 13, 21, 31) que corresponde al número 13

t_{3}=(3)^{2}+(3)+1

t_{3}=9+3+1=13

Con lo que podemos comprobar que la ecuación que obtuvimos cumple las reglas de nuestra sucesión, así que si quieres calcular el término para la posición numero 11 simplemente se tiene que sustituir el número 11 en las n.

Sígueme por Facebook, Tiktok, Twitter e Instagram